4.1 데이터에서 학습!
배우다 – 학습 데이터에서 가중치 매개변수의 최적 값을 자동으로 가져옵니다.
신경망 학습을 가능하게 하는 지표 → 손실 함수
현재 신경망의 매개변수는 무한하다 → 손으로 결정됨 X
4.1.1 데이터 기반 학습
기계 학습의 핵심 데이터 존재
그림에서 주어진 데이터로 해결) 특성 머신러닝 기술을 이용한 특징 패턴 추출 및 학습
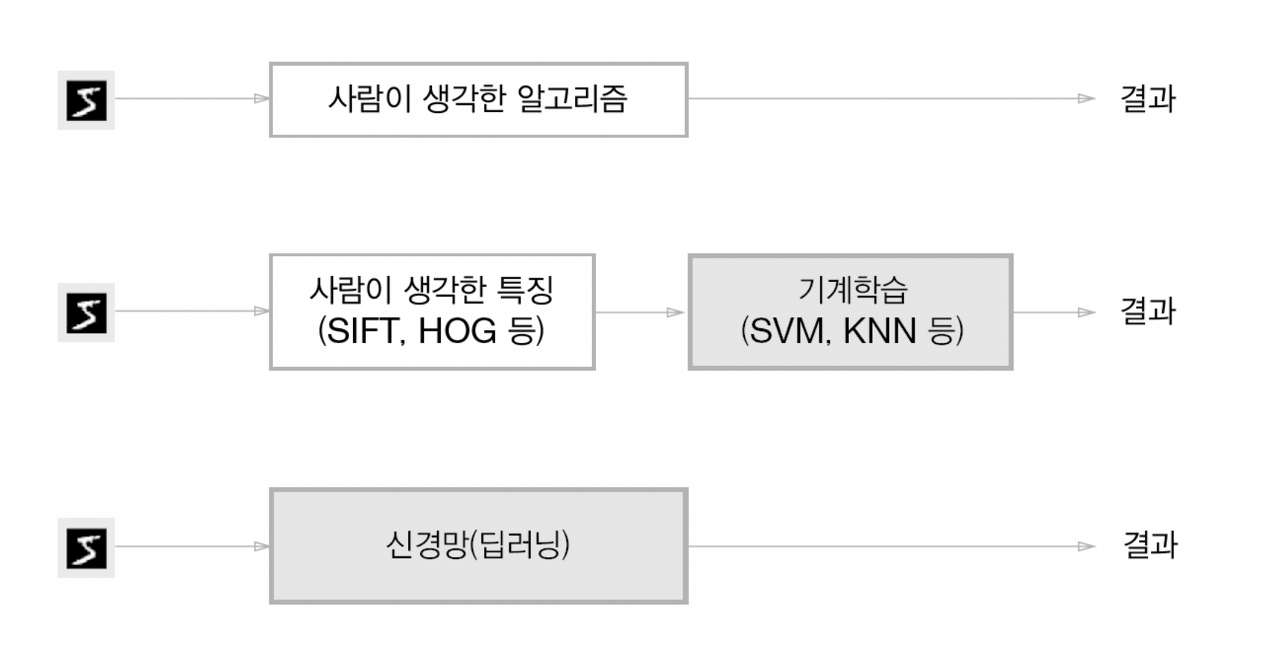
두 번째 접근 방식 – 기능의 인간 설계
세 번째 접근 방식 – 기능 맵의 “기계”가 스스로 학습합니다.
※ 종단 간(end-to-end) 기계 학습 – 사람의 개입 없이 데이터에서 목표 결과 얻기
4.1.2 교육 및 테스트 데이터
학습 데이터/테스트 데이터
훈련 데이터최적의 매개변수로만 학습
테스트 데이터학습된 모델의 성능 평가
왜?
보편적인 능력(아직 보지 못한 데이터로 문제를 정확하게 해결하는 능력)
과적합 단 하나의 데이터 세트에 대해 과도하게 최적화됨
4.2 손실 함수
“지표”를 기반으로 최적의 매개 변수 값 검색
신경망에서 사용하는 메트릭 → 손실 함수 (“나쁜” 신경망 성능의 지표)
4.2.1 오차 제곱합
오차 제곱합
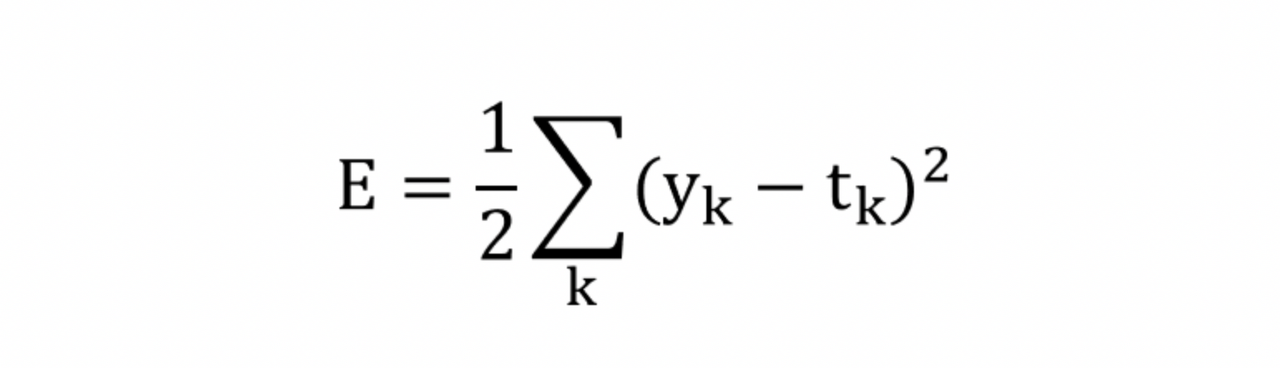
y_k – 신경망의 출력(신경망에 의해 추정됨)
t_k – 정답 라벨
k – 데이터의 차원 수
y = (0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0)
t = (0, 0, 1, 0, 0, 0, 0, 0, 0, 0)하나의 핫 인코딩 방법
정답을 가리키는 요소 1개 / 그렇지 않으면 0개
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)

첫 번째 예의 손실 함수 측 출력이 작음 = 올바른 레이블의 오류도 작음
4.2.2 교차 엔트로피 오류
교차 엔트로피 오류
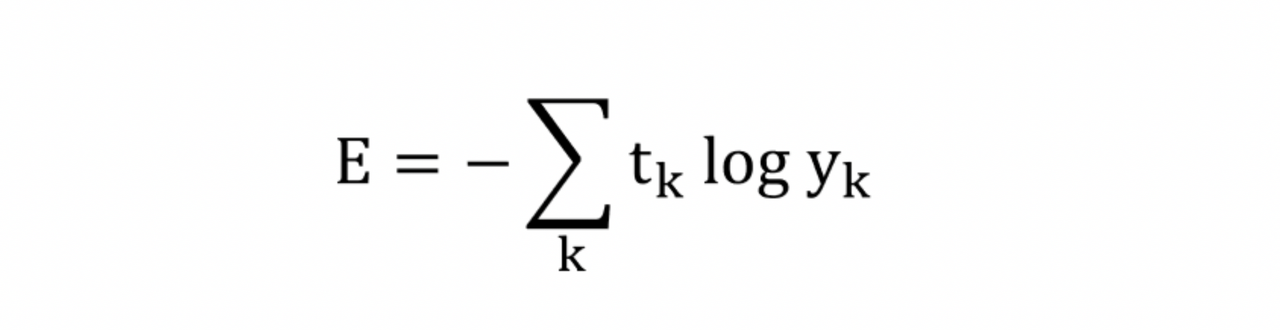
y_k – 신경망의 출력(신경망에 의해 추정됨)
t_k – 정답의 레이블(정답에 해당하는 인덱스의 요소만 1, 나머지는 0)
답이 실제로 맞을 때(t_k가 1일 때) 추정치의 자연 로그를 계산하기 위한 방정식
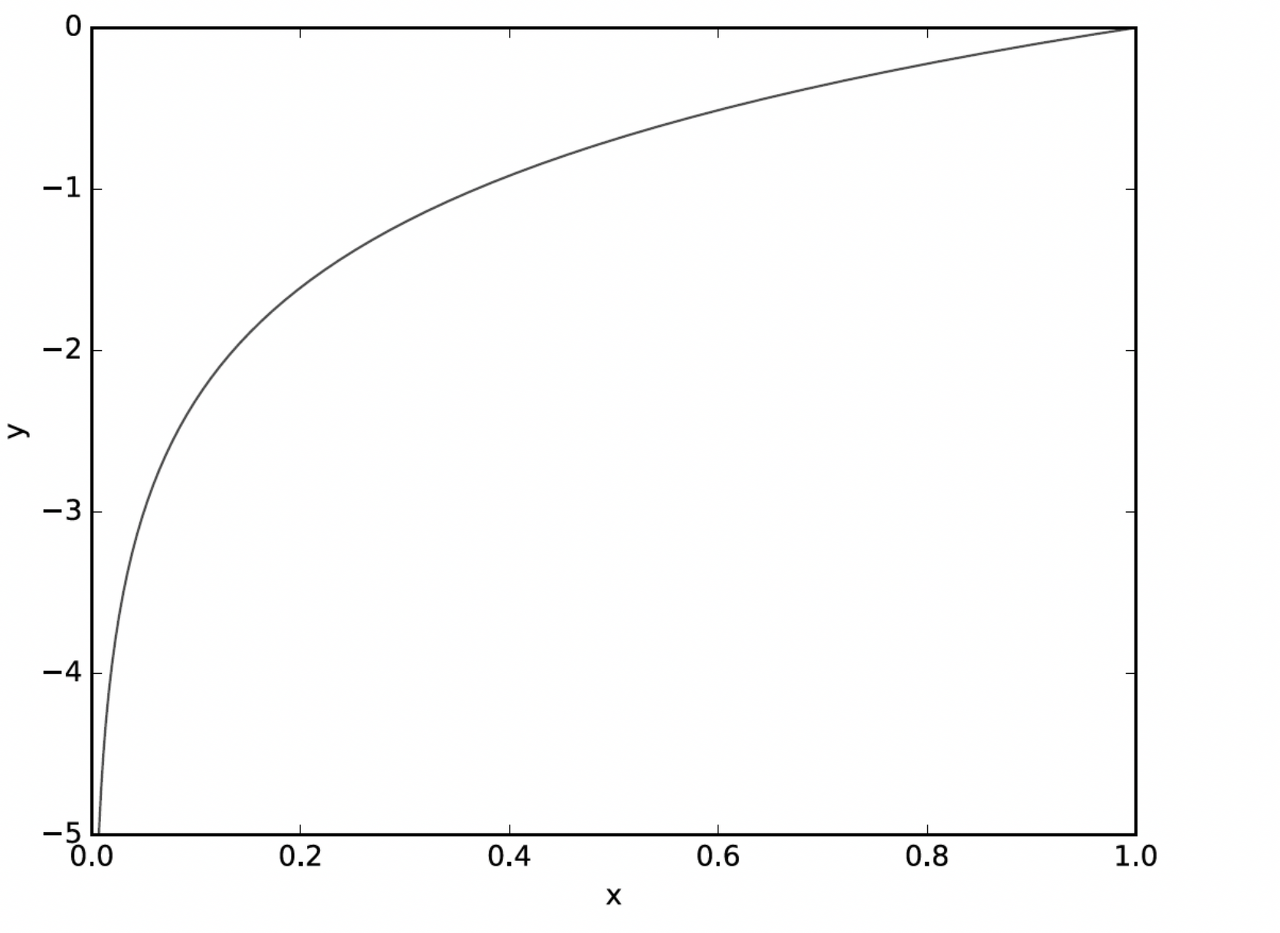
x가 0에 가까워지면 y의 값이 감소합니다.
정답에 해당하는 출력이 커질수록 0에 가까워짐 / 출력이 1일 때 0 → 정답이 작을 때 출력과 함께 오차가 커짐
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))np.log()에서 null 항목을 방지하기 위해 매우 작은 델타를 추가합니다.

오차 제곱합에 대한 판단에 동의
4.2.3 미니 배치 학습
교차 엔트로피 오류(두 훈련 데이터 모두 손실 함수의 합찾다)
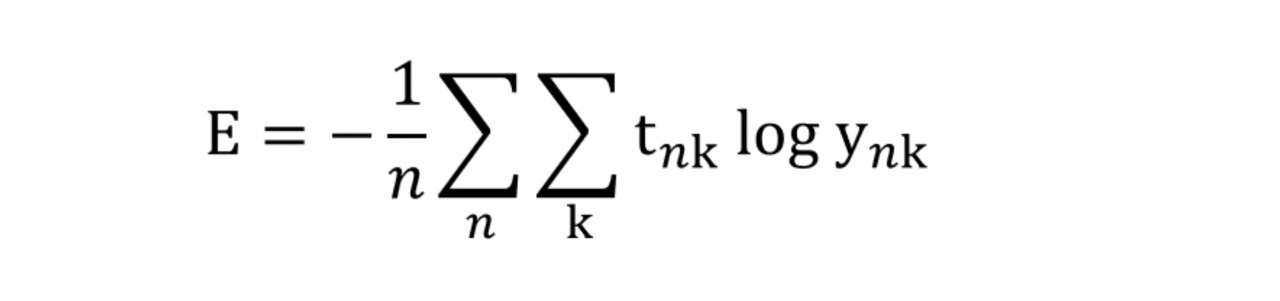
t_nk – n번째 데이터의 k번째 값
y_nk – 신경망의 출력
t_nk – 정답 레이블
1/n – N으로 나누기 ‘평균 손실 함수’찾았다
훈련 데이터에서 순수하게 신경 학습을 하는 경우에도 부분Teach-in만 선택하여 실행 – 미니 배치 훈련
일부 = 미니배치
train_size = x_train.shape(0) # 60000
batch-size = 10
batch_mask = np.random.choice(train_size, batch_size) # randomly select indecies from 0-59999
x_batch = x_train(batch_mask)
t_train = t_train(batch_mask)
'''
>>> np.random.choice(60000, 10)
array((8013, 14666, 58210, 10, 33333 ...))
'''np.random.choice() – 지정된 범위에서 원하는 숫자만 무작위로 검색
4.2.4 교차 엔트로피 오류 구현(배치용)
def cross_entropy_error(y, t):
if y.ndim == 1: # if dimension of y is 1
t = t.reshape(1, t_size)
y = y.reshape(1, y_size)
batch_size = y.shape(0)
return -np.sum(t * np.log(y + 1e - 7))y – 신경망의 출력
t-올바른 레이블
y는 1차원 – 데이터당 교차 엔트로피 오류 찾기 → reshape()로 데이터 모양 변경
비원 핫 인코딩
def cross_entropy_error(y, t):
if y.ndim == 1: # if dimension of y is 1
t = t.reshape(1, t_size)
y = y.reshape(1, y_size)
batch_size = y.shape(0)
return -np.sum(t * np.log(y(np.arange(batch-size), t) + 1e - 7))※ t=0인 요소의 경우 교차 엔트로피 오차도 0이므로 계산을 무시해도 됩니다.
4.2.5 손실 함수를 설정하는 이유는 무엇입니까?
“정확도”라는 메트릭 대신 ‘손실 함수 값’ 사용.
왜?
신경망 학습에서 최적의 매개변수를 찾을 때는 손실함수의 값을 최대한 작게 만드는 매개변수 값을 찾는다.
→ 매개변수의 미분을 계산합니다. → 차이 값을 기준으로 단계별로 파라미터 값을 업데이트하는 과정을 반복
가중치 매개변수의 손실함수의 미분 = ‘가중 매개변수의 값이 아주 조금만 변하면 손실함수는 어떻게 변하는가?’
정밀도는 대부분의 경우 미분이 0이므로 업데이트할 수 없는 매개변수입니다.
단계 함수 – 값이 이산적으로 변경됨(대부분의 위치에서 기울기 없음)
시그모이드 기능 – 값이 계속 변하고 곡선의 기울기도 계속 변합니다(기울기가 0이 되지 않음).
4.3 수치 미분
기울기 값을 기준으로 이동 방향 설정
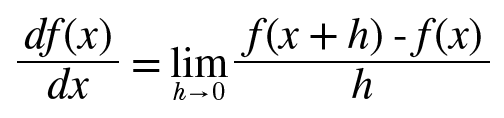
미분 – 순간의 변화량을 보여줍니다.
def numerical_diff(f, x):
h = 1e-50
return (f(x+h) - f(x)) / h※ 개선사항
1. 반올림 오류 – Float32로 표현되는 1e-50은 0.0입니다.
2. f의 차이 – (x+h)와 x 사이의 기울기는 정확히 진정한 도함수 X입니다.
(x+시간) (x시간)
x를 중심으로 전후 차이를 계산합니다 – 중심 차이 또는 중심 차이
(x+h) x – 순방향 차이
def numerical\_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2\*h)4.3.2 수치 미분의 예
def function\_1(x):
return 0.01\*x\*\*2 + 0.1\*x
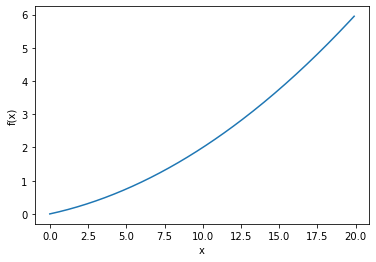
>>> 0.1999999999990898
>>> 0.2999999999986347실제 미분 – 0.2, 0.3
4.3.3 부분 미분
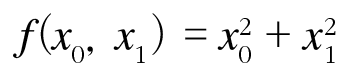
def function_2(x):
return x(0)**2 + x(1)**2
# 또는 return np.sum(x**2)x-numpy 배열
부분 도함수 – 다변량 함수의 도함수
# x0=3 및 x1=4인 경우 x0에 대한 편미분 af/ax0
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
print(numerical_diff(function_tmp1, 3.0))
>>> 6.00000000000378# x0 = 3 및 x1 = 4인 경우 x1에 대한 편도함수 af/ax1
def function_tmp2(x1):
return 3.0**2.0 + x1*x1
print(numerical_diff(function_tmp2, 4.0))
>>> 7.999999999999119
4.4 경사
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같은 배열 생성
for idx in range(x.size):
tmp_val = x(idx)
# f(x+h) 계산
x(idx) = tmp_val + h
fxh1 = f(x)
#f(x-h) 계산
x(idx) = tmp_val - h
fxh2 = f(x)
grad(idx) = (fxh1 - fxh2) / (2*h)
x(idx) = tmp_val # 값 복원
return grad연산 방식 – 변수가 하나일 때 수치 미분과 거의 동일
np.zero_like(x) – 요소가 모두 0인 x와 동일한 모양의 배열을 만듭니다.
f – 함수 / x – numpy 배열
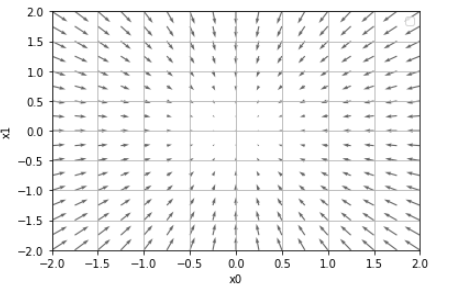
- 방향이 있는 벡터로 그려짐
- 그래디언트는 함수의 ‘최저점'(최소)을 가리킵니다.
- 화살표는 “가장 낮은 지점”에서 멀어질수록 커집니다.
기울기는 각 위치에서 함수의 출력을 가장 많이 줄이는 방향을 가리킵니다.
4.4.1 기울기 방법(기울기 하강법)
매개 변수 공간이 큽니다. 최소 X가 어디에 있는지 추측하십시오.
→ 이런 상황에서 그래디언트를 이용하여 함수의 최소값을 찾아보세요 = 그라데이션 방법
각 지점에서 함수의 값을 줄이는 방법을 제안하는 지표 – 경사 (보증 ×)
그라데이션 방법 – 현재 위치에서 기울어진 방향으로 지정된 거리만큼 이동
이동한 곳에서 기울기를 구하여 기울어진 방향으로 이동을 반복 → 서서히 함수값을 감소
찾은 최소값 – 경사 하강법
최대 발견 – 경사 오르기
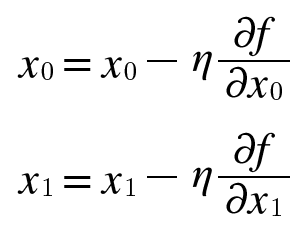
eta – 업데이트할 양
def gradient_descent(f, init_x, lr = 0.01, step_num = 100):
x = init_x
for i in range(step_num):
grad = numerial_gradient(f, x)
x -= lr * grad
return xinit_x – 초기값
lr – 학습률, 즉 학습률을 의미합니다.
step_num – 그래디언트 방법에 따른 반복 횟수
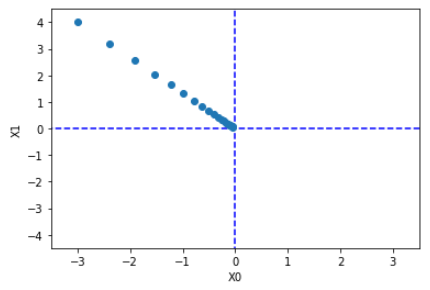
값이 낮은 원점에 점차 가까워짐
- 학습률이 너무 크면 큰 값으로 발산한다.
- 학습률이 너무 낮으면 거의 업데이트되지 않습니다.
※초매개변수 – 학습률과 같은 매개변수, 사람이 수동으로 설정해야 하는 매개변수
여러 후보 값 중에서 테스트를 통해 학습이 잘 되는 값을 찾는 과정을 거친다.
4.4.2 신경망의 기울기
신경망의 기울기 = 가중치 매개변수에 대한 손실 함수의 기울기
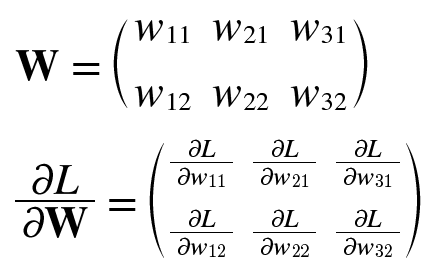
가중치는 W, 손실 함수는 L
행 1의 첫 번째 요소 – W11이 약간 변경될 때 손실 함수 L이 얼마나 변경되는지 알려줍니다.
모양 W 2×3과 동일
심플넷 클래스
class simpleNet:
def __init__(self):
self.W = np.random.randn(2, 3) # init with normal distribution
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss인스턴스 변수로 2×3 형식의 가중치 매개변수를 가집니다.
2가지 방법
예측하다 (x) – 예측하다
loss(x,t) – 손실 함수를 평가합니다.
x 입력 데이터
t – 정답 레이블
f= lambda w: net.loss(x,t)
dW= numerical_gradient(f, net.W)신경망의 기울기 구하기 → 기울기 방법에 따라 가중치 매개변수 업데이트
